Difference between revisions of "Setting Steps per mm"
(→Equation) |
(→Equation) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 18: | Line 18: | ||
<code>New_Value = Current_Value / Actual_Distance * Desired_Distance</code> | <code>New_Value = Current_Value / Actual_Distance * Desired_Distance</code> | ||
| − | So if the current value for X was 80 and the printer only moved 97mm when trying to move 100mm, the equation would be: <code> | + | So if the current value for X was 80 and the printer only moved 97mm when trying to move 100mm, the equation would be: <code> 80 / 97 * 100</code> |
| − | The new X Steps Per mm to | + | The new X Steps Per mm to 82.47. |
The same principle applies for the extruder. If over/under-extruding, use this equation. | The same principle applies for the extruder. If over/under-extruding, use this equation. | ||
Latest revision as of 12:24, 18 March 2016
Procedure
This is a great way to fix problems with the printer not moving the expected distance, or having parts come out with incorrect dimensions.
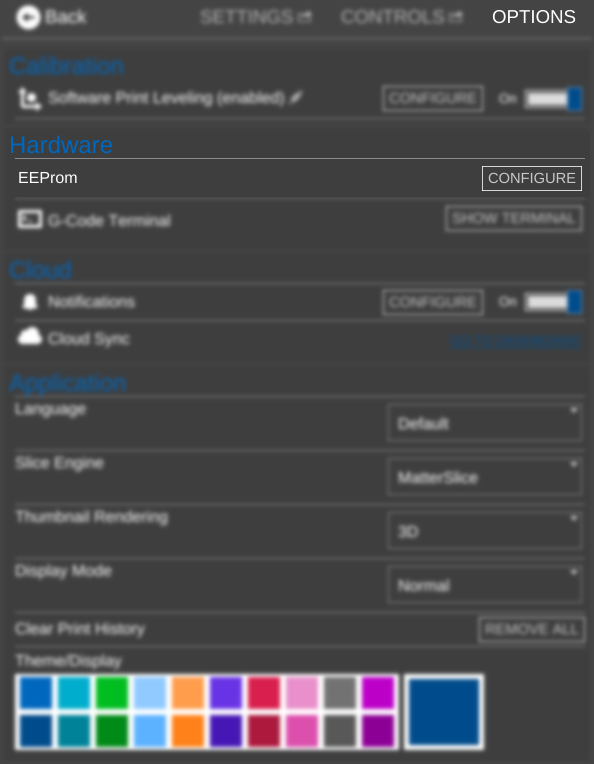
- Navigate to

- Click on the
 tab
tab - Connect to your printer
- In the EEProm section click on

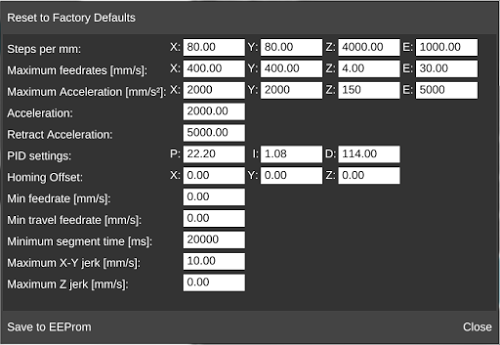
- Change the Steps per mm to correct for any discrepancy you find in your movement distances.

Equation
Here is the equation to find the correct value:
New_Value = Current_Value / Actual_Distance * Desired_Distance
So if the current value for X was 80 and the printer only moved 97mm when trying to move 100mm, the equation would be: 80 / 97 * 100
The new X Steps Per mm to 82.47.
The same principle applies for the extruder. If over/under-extruding, use this equation.
Cartesian vs. delta
Steps per mm settings will be different for Cartesian printers vs. delta printers.
Cartesian printers have one value for each axis. This means there will be a Steps per mm (X), Steps per mm (Y), and Steps per mm (Z). Each will be different, and will require the above calculation to determine the correct value.
Delta printers only have one Steps per mm field because all three motors work in conjunction to triangulate the position of the nozzle. Thus, only one calculation is needed if the dimensions of the printed part differs from those of the model. If measured independently, they should all be off by the same ratio. If not, the problem lies elsewhere.